Pregunta transcendental donde las hayan, ¿verdad? Vale, tampoco es para tanto. Pero me sirve de argumento para poner a trabajar a mi ordenador un rato y para refrescar conocimientos de machine learning.
Datos
Me he descargado una base de datos de alimentos con sus valores nutricionales y sus contenidos en vitaminas, etc de myfooddata.com a través de la USDA Agricultural Research Service (el servicio de investigación agricultural del Departamento de Agricultura de los Estados Unidos).
Una base de datos con 6.347 observaciones (alimentos) y 56 variables descriptivas (componentes, vitaminas, energía, etc.).
USDAfoods <- read.csv("inputData/USDAfoodFacts.csv", sep = ";")
Alcance del estudio
Para el análisis que quiero hacer, me he quedado con todos los alimentos de la categoría “Finfish and Shellfish Products“, esto es, 264 observaciones con 56 variables. No es para echar cohetes pero es todo lo que he encontrado.
USDAfish <- USDAfoods %>%
dplyr::filter(Food.Group == "Finfish and Shellfish Products")
Preparación de los datos
Los datos vienen muy limpios pero es necesarios realizar unos pocos ajustes, que resumo a continuación.
- Selección de variables: me quedo con aquellas columnas en las que la mayoría de las observaciones presentan valores no nulos y distintos de 0. Me quedo con 32 variables.
USDAfish <- USDAfish[c(1:8,16,22:35,45:55)]
- Conversión de las comas decimales a puntos para convertir las variables a numéricas posteriormente.
for (i in 4:ncol(USDAfish)) {
USDAfish[,i] <- as.character(USDAfish[,i])
USDAfish[,i] <- stringr::str_replace_all(USDAfish[,i], ",", "\.")
}
- Conversión de las variables explicativas en variables numéricas.
for (i in 4:ncol(USDAfish)) {
USDAfish[,i] <- as.numeric(as.character(USDAfish[,i]))
}
- Normalización las variables explicativas.
normalize = function(x) {
return ((x - min(x)) / (max(x) - min(x)))
}
USDAfish_Norm <- as.data.frame(lapply(USDAfish[,4:32], normalize))
¿Comenzamos con el aprendizaje automático?
Análisis de componentes principales: ACP o PCA en inglés
Se trata de un método no supervisado, los datos no están etiquetados, esto es, el ordenador no sabe a priori si un pescado es blanco o azul. En esencia, este método busca reducir la dimensionalidad del conjunto de datos sacrificando la mínima varianza posible. Convierte mi conjunto de 29 variables en un conjunto de componentes que son una combinación lineal de las primeras.
Para poder hacer una representación “fiel” en 2 dimensiones, necesitamos que las 2 primeras componentes representan una gran cantidad de la variabilidad de los datos de origen.
En este caso, no es así ya que las dos primeras componentes tan solo capturan el 34% de la variabilidad de los datos.
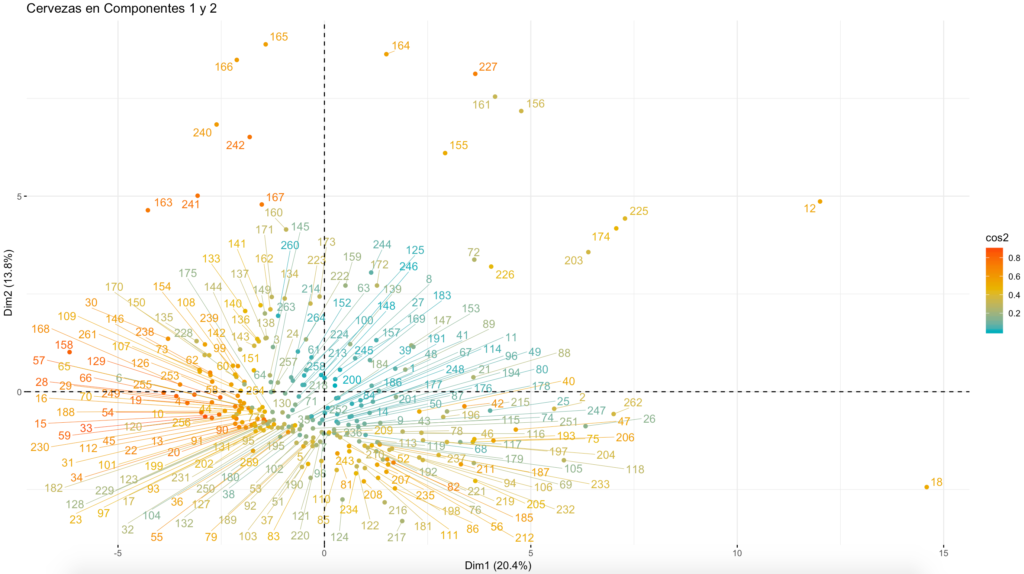
Tampoco podemos discernir 2 o 3 grupos de puntos claramente definidos, como cabría esperar.
KNN – K nearest neighbours o los k – vecinos más cercanos
Este algoritmo forma parte de los métodos de aprendizaje supervisado por lo que, previamente, tenemos que etiquetar nuestros pescados. En este caso, he establecido 3 categorías: blanco, azul y semigraso.
Divido mi nuestra en dos grupos: entrenamiento (80%) y test (20%) y aplico el algoritmo, eligiendo un valor de k = 3. Simplificando, k representa el número de vecinos (observaciones) que vamos a tener en cuenta a la hora de decidir la clase de mi elemento de test.
split <- 0.80
trainIndex <- createDataPartition(USDAfish$tipo, p=split, list=FALSE)
etiquetas <- USDAfish$tipo
train <- USDAfish_Norm[trainIndex,]
trainlabels <- etiquetas[trainIndex]
test <- USDAfish_Norm[-trainIndex,]
testlabels <- etiquetas[-trainIndex]
Ahora aplicamos el algoritmo y contratamos en una tabla los resultados obtenidos con las etiquetas reales de los pescados:
out <- knn(train, test, trainlabels, k = 3, prob=TRUE)
tab <- table(out, testlabels)
print(tab)
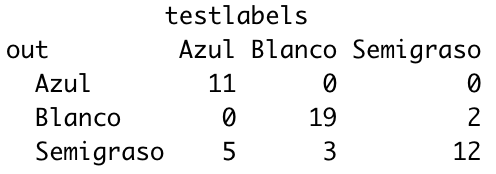
¿Qué tal ha ido?
- En los azules, ha fallado en 5 (de 16), que se han ido a semigrasos.
- En los blancos ha fallado en 3 (de 22), que se han ido a semigrasos.
- En los semigrasos ha fallado en 2 (de 14), que se han ido a blancos.
¿Lo medimos en términos de eficacia?
mean(out == testlabels)
Ha acertado en un 80%. No está mal.
K-means
K-means es otro algoritmo de aprendizaje no supervisado o clusterización. Esto es, un algoritmo que va a agrupar nuestras observaciones en K grupos. En este caso, he impuesto que K sea igual a 3.
set.seed(20)
fishCluster <- kmeans(USDAfish_Norm, 3, nstart = 20)
fishCluster
K-means nos devuelve unos cuántos datos:
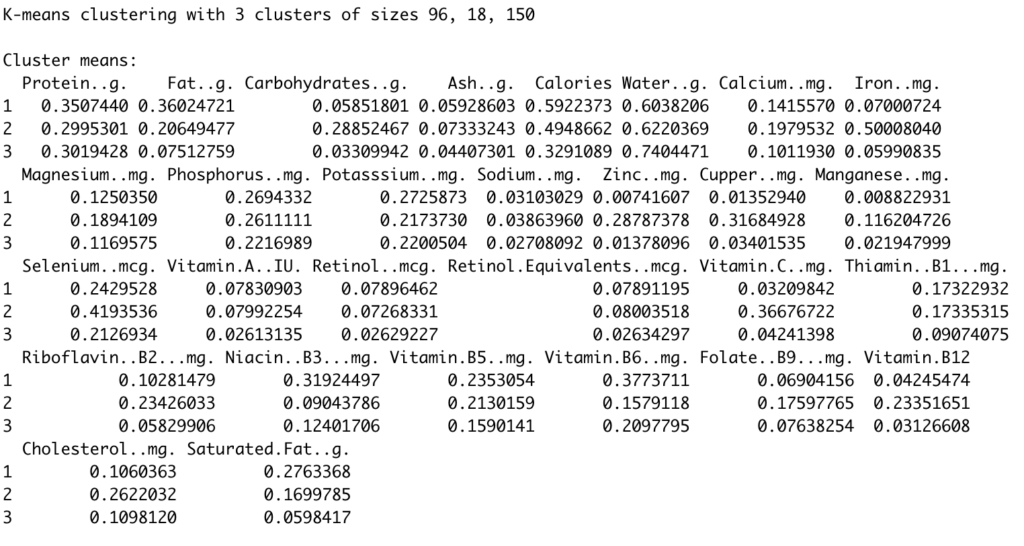

Hemos obtenido 3 clusters (se lo habíamos indicado así) de 96, 18 y 150 pescados respectivamente.
Cuando tenemos más de dos variables, para poder representarlo, tenemos que aplicar PCA (lo hemos hecho antes) para representar las dos primeras componentes. Lo podemos hacer mediante el siguiente comando:
fviz_cluster(fishCluster, data = USDAfish_Norm)
Este es el resultado:
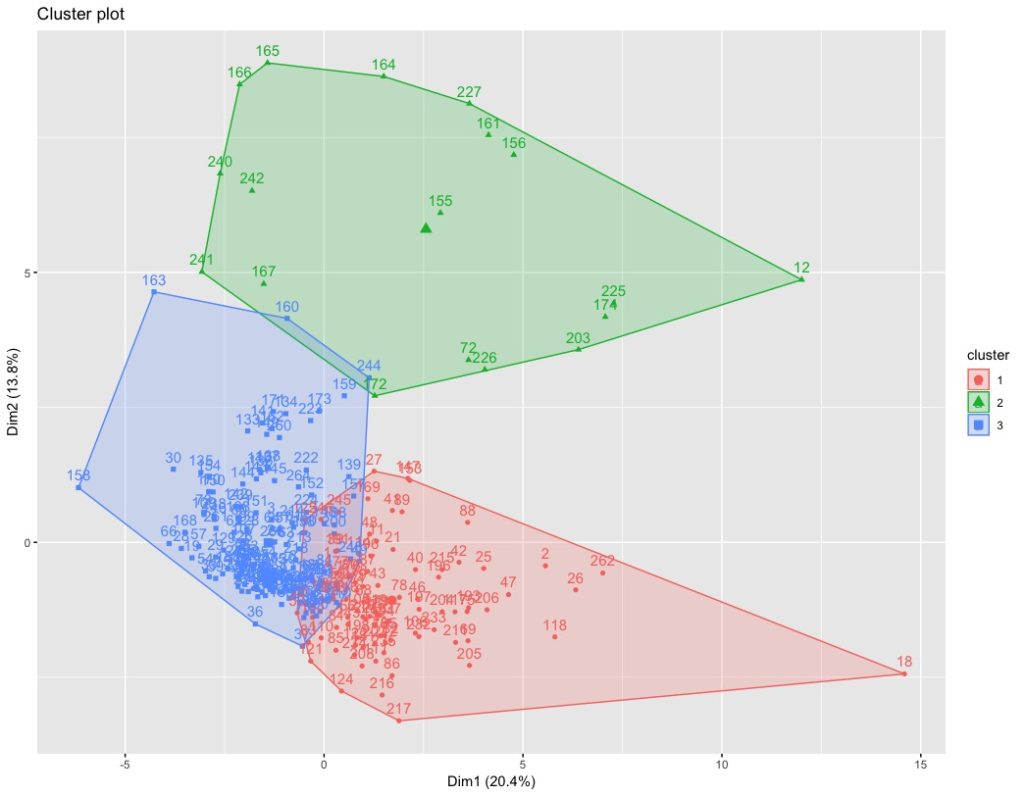
El cluster número 2 (verde) queda muy bien retratado, con una ligera interferencia con el cluster 3 (azul).
Los clusters 3 (azul) y 1 (rojo) tienen una zona común demasiado grande.
Podemos ver los resultados del test en forma de tabla, como hacíamos con knn:

Los resultados no son demasiado buenos. Los pescados azules quedan bien retratados en el cluster 1; los pescados blancos quedan bien retratados en el cluster 3; los pescados semigrasos no quedan muy bien retratados.
Para poder calcular un valor de eficacia como hacíamos con knn, tendremos que asignar los nombres de los tipos de pescados a los números de clusters (1-Azul; 2-Semigraso; 3-Blanco).
fishCluster$cluster2 <- ifelse(fishCluster$cluster == 1, "Azul",
ifelse(fishCluster$cluster == 2, "Semigraso", "Blanco"))
mean(fishCluster$cluster2 == USDAfish$tipo)
Ha acertado en un 69%.
Antes de aplicar K-means suele ser recomendable calcular cuál es el número óptimo de clusters que dividen a mi muestra. En esta ocasión no lo he hecho porque tenía “claro” que mis pescados pertenecen a 3 categorías. Aunque quizás la categoría semigrasos no esté del todo bien definida.
De hecho, si calculamos el número óptimo de clusters, el resultado es 2:
fviz_nbclust(USDAfish_Norm, kmeans, method = "silhouette")
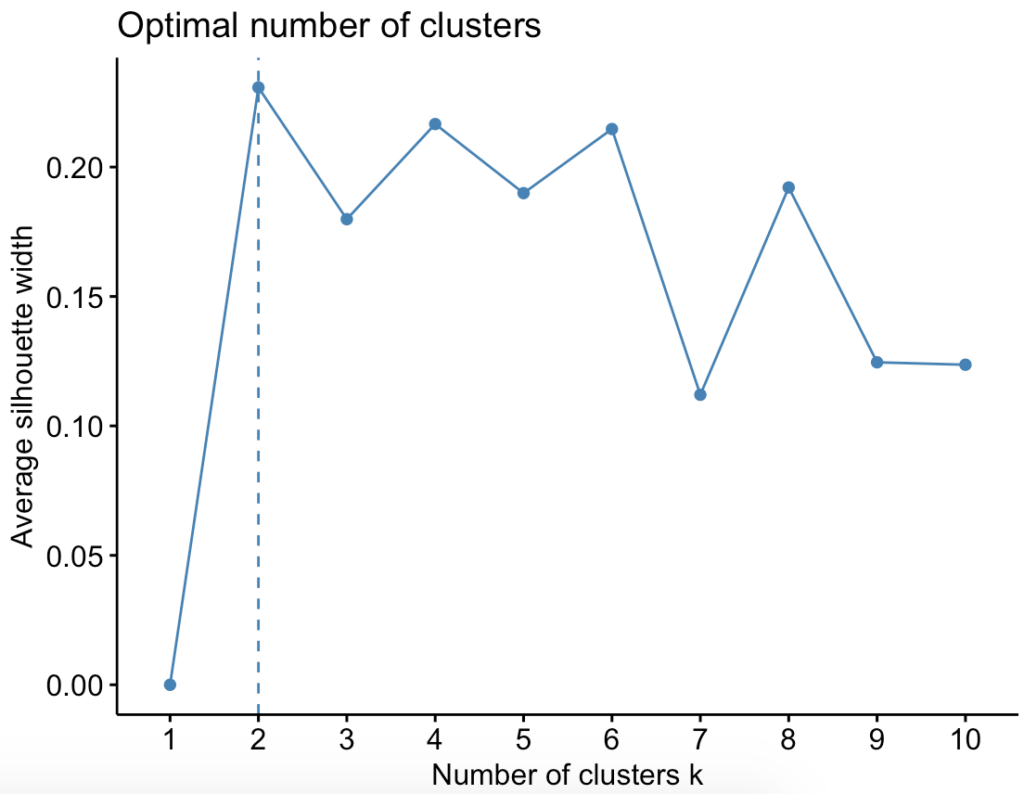
Clusterización jerárquica
Vamos a finalizar probando con un árbol de decisión, un algoritmo de clasificación que cuenta con la ventaja de ser muy explicativo. Volvemos al aprendizaje supervisado.
indice = createDataPartition(USDAfish$tipo, p = 0.8, times = 1, list=TRUE)
datostra = USDAfish[ indice[[1]], ]
datostst = USDAfish[-indice[[1]], ]
modelotree1 = rpart(tipo~., data = datostra[,4:33], method = "class", maxdepth=4)
modelotree1
# visualización del árbol de decisión
par(mfrow=c(1,1))
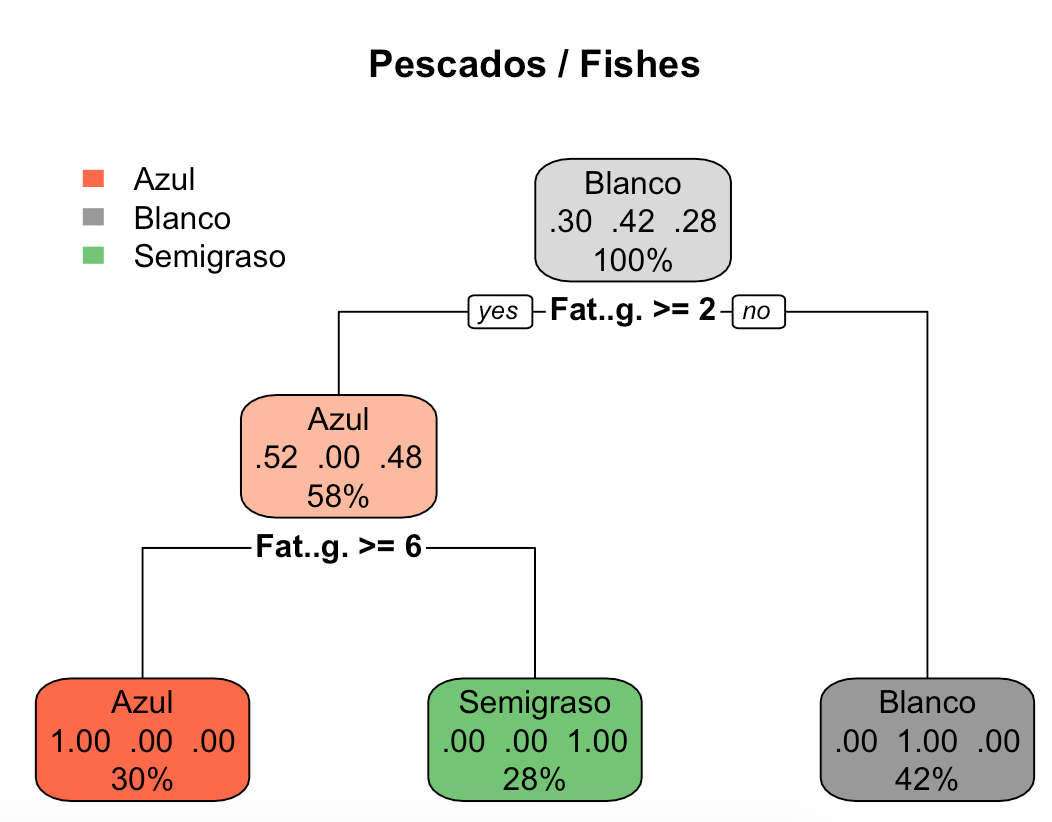
rpart.plot(modelotree1, main="Pescados / Fishes")
Este es el resultado:
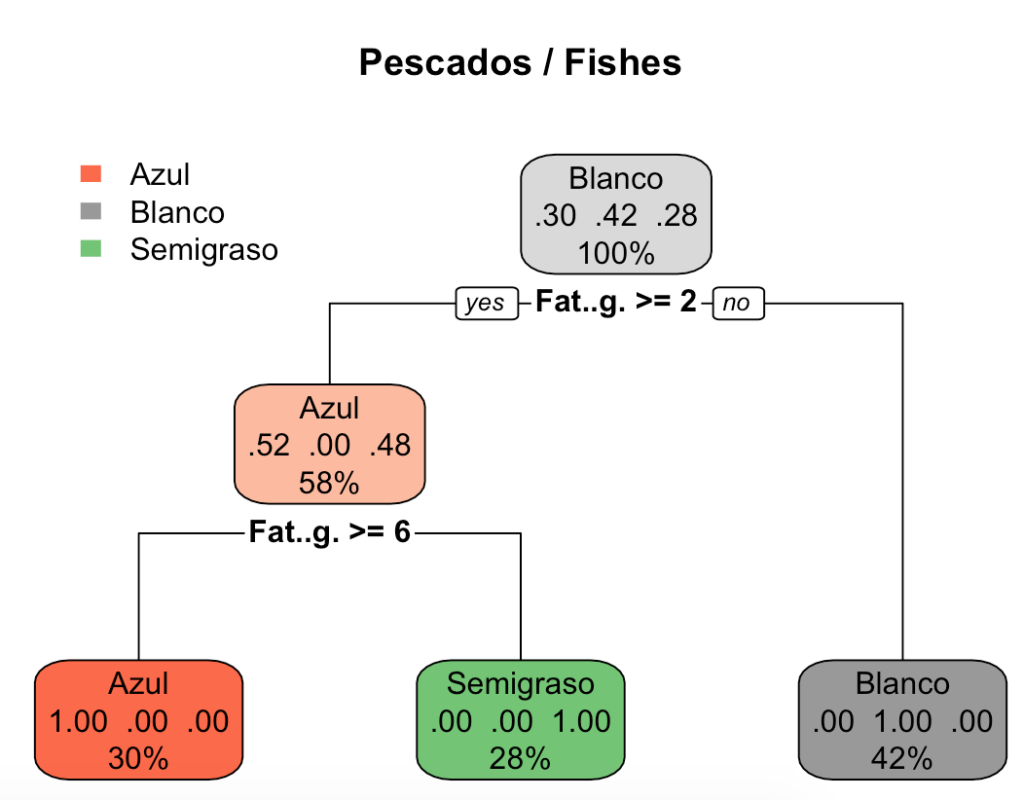
Como véis, el algoritmo ha dividido los pescados en función de su contenido de grasa:
- Grasa (Fat..g.) < 2 g (por cada 100 gramos): pescado blanco.
- Grasa (Fat..g.) >=2 g (por cada 100 gramos) y <6 g: pescado semigraso.
- Grasa (Fat..g.) >= 6 g (por cada 100 gramos): pescado azul.
Y lo mejor de todo es que los ha clasificado con un acierto del 100%.
#r #rstudio #datacy #datadrivendecisions #machinelearning #aprendizajeautomatico #cluster #fish #pescados #datascience #bigdata #datascientist #mineriadedatos #blancooazul #kmeans #knn #arboldedecision #decisiontree #pca #acp #principalcomponentsanalysis #analisisdecomponentesprincipales