Con motivo de la celebración del día internacional de la mujer el pasado viernes, se me ocurrió realizar una escucha en Twitter. Como suelo hacer siempre, primero me documento sobre el tema para buscar las palabras (hashtags) más relevantes sobre el tema que quiero escuchar.
Navegando por Internet me encontré con esta noticia en la que, en resumidas cuentas, contaba cómo Podemos y PP se preparaban para las movilizaciones del 8M. Cada partido con su hashtag, a modo de batalla por la supremacía en del feminismo. No huele a elecciones ni nada.
Decidí aprovecharme de la “pelea” y decidí escuchar ambos hashtags. Como las escuchas en streaming consumen muchos recursos, descargué los tweets a posteriori, haciendo dos descargas de 3.200 tweets para cada hashtag.
Estas son las cifras totales:
- #NadaNosPara8M (el hashtag de Podemos): 5.801 tweets entre las 8:30:04 y las 13:49:16.
- #NoHablamosHacemos (el hashtag de Podemos): 5.539 tweets entre las 20:36:06 (7 de marzo) y las 13:50:39 (8 de marzo).
En esta ocasión he enfocado el análisis desde el punto de vista de la teoría de grafos, con el objetivo de analizar la estructura de cada una de las redes creadas.
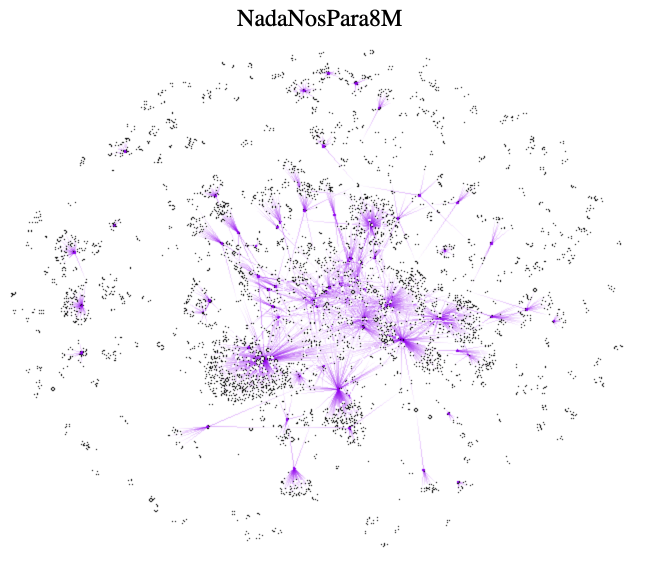
#NadaNosPara8M – Podemos:
Cada nodo es un usuario de Twitter y cada arista un retweet entre el nodo origen y el nodo destino. Este es el grafo en bruto, sin sin asignar ningún atributo a los nodos. A simple vista se puede apreciar cómo de algunos nodos salen muchas aristas y cómo algunos nodos reciben muchas aristas. Vamos, que algunos nodos parecen más importantes o, como se suele decir en el mundo de las redes sociales, influyentes (influencers).
Se trata de una red con 3.352 nodos (usuarios únicos de Twitter) y 3.625 aristas. Algunos de sus parámetros son:
- Densidad: 0,032%. De todas las posibles aristas (si todos los usuarios estuvieran conectados con todos), la red sólo dispone del 0,032% de las mismas. ¿Es mucho o poco? La mejor forma de calcularlo es confrontarlo con otros grafos similares. Esto es relativamente sencillo de calcularlo con programación en, por ejemplo, R. Confrontamos la distancia media de nuestro grafo con la de 1.000 grafos aleatorios con parámetros similares (igual número de nodos y densidad aproximadamente igual). Este es el resultado:

- Distancia media: 1,63 saltos (aristas). ¿La comparamos con nuestras redes aleatorias?

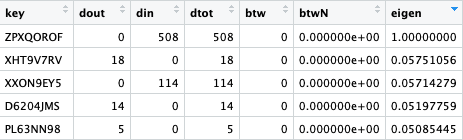
También podemos detectar a los usuarios más influyentes gracias a ciertos parámetros derivados de sus comportamiento en la red (he pseudonimizado los nombres de usuario por protección de datos):
- Grado o número de conexiones: conexiones entrantes (retweets recibidos), salientes (retweets realizados) y totales (la suma de ambas). Top5 usuarios (anonimizados):
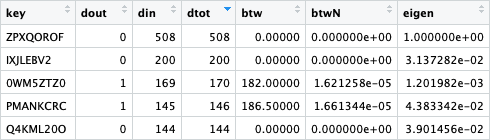
- Betweenness: mide la importancia de un nodo (usuario) en la red desde el punto de vista del flujo de información. Cuanto más alto sea el valor del parámetro, más relevante será el usuario para la conectividad global de la red.
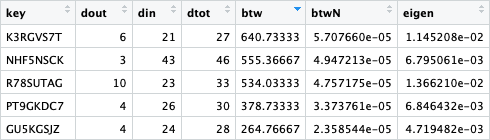
- Eigenvector: mide lo bien conectado que está un nodo, especialmente, lo bien conectado que está con otros nodos que, a su vez, están bien conectados.
Gracias al paquete graphjs y a la función threejs de R, podemos plotear las redes de forma interactiva. Esta es la red sin asignar pesos a los nodos. Podéis girarla y hacer zoom para acceder a cualquier nodo.
En la siguiente animación, el tamaño de los nodos es proporcional a su valor Eigen, a su poder de influencia en la red:
Como véis, hay 1 nodo (usuario) que destaca sobre los demás. Interesante, ¿verdad?
Estas son las palabras más utilizadas en los tweets recogidos en forma de nube de palabras:

Próximamente el análisis del hashtag del PP.